Jainism has some powerful Mantras like ‘Navkar Mantra’, which is the most powerful than the others. But today we’ll talk about the Mantra composed by the great Acharya Pujya BhadhraBahu Swami, who lived in around 2nd to 4th century AD, ‘Uvasaggaharam Stotra’. It is believed to eliminate obstacles, hardships, and miseries, if chanted with complete faith. This Sutra is associated with its ‘Yantra’, known as ‘Uvasaggaharam Yantra’. At the centre if this Yantra there is a Magical 5×5 Magic Square with many peculiarities and specialities.
Note: A magic square is a ‘n x n’ square grid (where ‘n’ is the number of cells on each side) filled with distinct positive integers in the range 1,2,…,n2 such that each cell contains a different integer and the sum of the integers in each row, column and diagonal is equal. The sum is called the ‘Magic Constant’ or ‘Magic Sum’ of the magic square.
- Numbers used in the Magic Square
- Number of ways we get the ‘Magic Constant’
- The Yantra Itself
Let’s discuss them all.
Numbers used in the Magic Square
Per definition, a normal magic square of ‘n x n’ will have numbers with the below specifications: –
- Numbers are in sequence
- Numbers starting from 1
- Up to n2
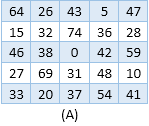
Figure (A) shows the ‘Uvasaggaharam Magic Square’ known as non-normal magic square.
On initial look it seems it has some random numbers.
- Numbers are out of sequence
- Numbers are starting from 0
- Up to 3n2-1
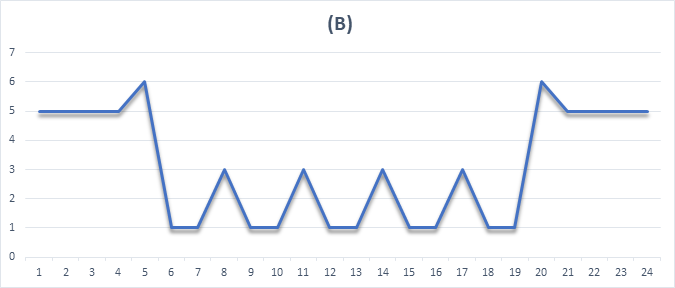
Here are the numbers in ascending order – [0,5,10,15,20,26,27,28,31,32,33,36,37,38,41,42,43,46,47,48,54,59,64,69,74] which doesn’t give any pattern. But when we take the difference of the consecutive numbers (m – m-1) we have beautiful palindrome number sequence – [5,5,5,5,6,1,1,3,1,1,3,1,1,3,1,1,3,1,1,6,5,5,5,5]. Plotting a line graph in Figure (B) which is symmetric on ‘Y’ axis, meaning there is a sequence/pattern followed.
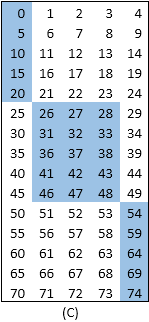
Trying a different approach, write all the number from 0 to 74 in group of 5 and highlighting the magic numbers give the ‘Glide Reflection Symmetric’ Figure (C)
Number of ways we get the ‘Magic Constant’
Per definition, a regular 5×5 will have a magic constant of 65, but this ‘Uvasaggaharam Magic Square’ has it as 185. Since the ‘Uvasaggaharam Sotra’ has 185 characters the Magic Square is constructed for the constant of 185. A normal 5×5 magic square has 12 different quintets to get the magic constant as 65. Let’s see how many ways we get 185.
Considering the rows
Figure (1) to (5) shows all the individual rows adds up to 185

Considering the Columns
Figure (6) to (10) shows all the individual rows adds up to 185

Considering the Diagonals
Diagonals are further divided into 2 parts
Normal Diagonals
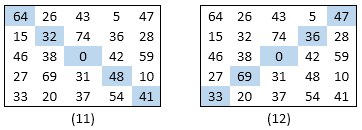
Figure (11) and (12) shows the 2 normal diagonals adds up to 185
Broken Diagonals
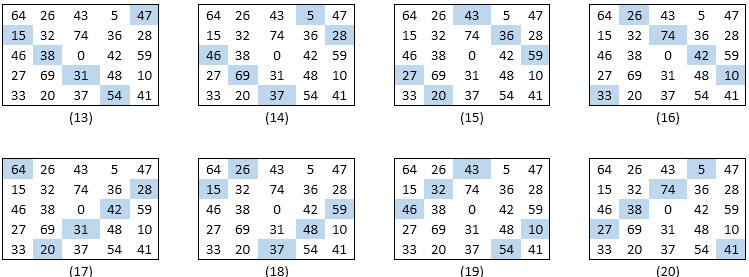
A Broken diagonal is a set of n cells forming two parallel diagonal lines in the square. Alternatively, these two lines can be thought of as wrapping around the boundaries of the square to form a single sequence. Figures (13) to (16) & (17) to (20) corresponds to the 2 sets of Broken Diagonal making this Magic Square as ‘Pandiagonal Magic Square’
Subset of 3×3
Every 5×5 square has 9 different 3×3 internal squares as show below in figures ‘a’ to ‘i’.
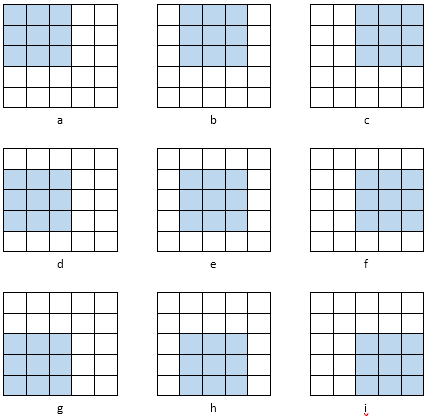
And each of these 3×3 squares has 2 set of quintets as below.
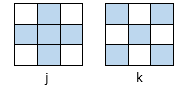
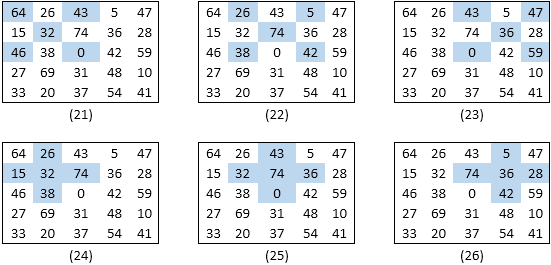
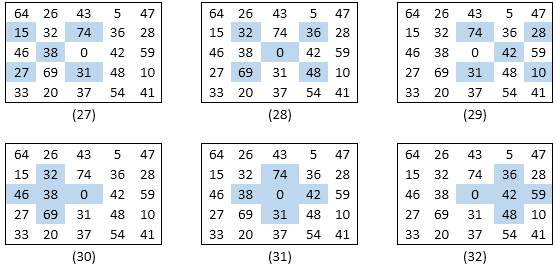
Thus we have total of 18 new quintets with the sum of 185 as shown in figures (21) to (38)
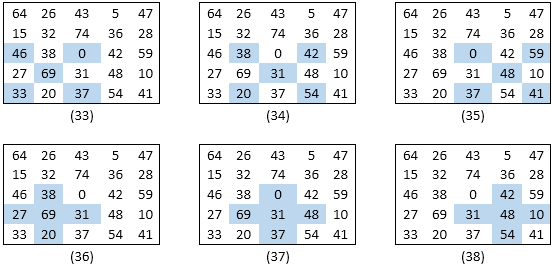
Special Ones
In the above all the 3×3 the 2 quintets are formed as
- 4 Edges and the Centre of the 3×3
- 4 Corners and the Centre of the 3×3
Applying the same logic to 5×5 square we get 2 more quintets of 185, Figures (39) and (40)
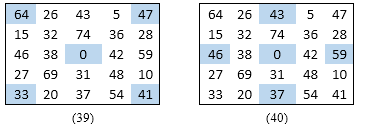
In this way we see a total of 40 Quintets formed in this 5×5 Magic Square.
Bonus
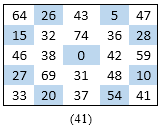
The Scriptures of this Yantra were having a very good hold in Maths and they hide a group of 9 digits to give a sum of 185 – 4 Broken Diagonals and a Centre. Figure (41)
Author: Bhavin Mehta
Jainuine_admin
Related posts
3 Comments
Leave a Reply Cancel reply
Today's pick
Hot topics
Stay connected
Notice: Trying to get property 'data' of non-object in /home/jainuine/public_html/wp-content/themes/gillion/inc/widgets/social-counter/views/widget.php on line 36
Notice: Trying to get property 'counts' of non-object in /home/jainuine/public_html/wp-content/themes/gillion/inc/widgets/social-counter/views/widget.php on line 36
Notice: Trying to get property 'followed_by' of non-object in /home/jainuine/public_html/wp-content/themes/gillion/inc/widgets/social-counter/views/widget.php on line 36


that’s a type of secret which you had explained. keep uploading such contents!
Oh great . Great efforts n research . It’s really amazing to see any mantra in such way.pl keep it up.pl add me if u created any group to post such things.
u can connect us on whatsapp group also – 9853098930